Data Structures & Algorithms in Swift Full Release Now Available!

Hey, Swifties! The full release of our Data Structures & Algorithms in Swift book is now available!

The early access release of this book — complete with the theory of data structures and algorithms in Swift — debuted at our conference RWDevCon 2018. Since then, the team has been hard at work creating a robust catalogue of challenges — 18 chapters in all — to test what you’ve learned and grow your expertise. The book is structured with the theory chapters alternating with the challenge chapters to keep you on track to nail down the fundamental and more advanced concepts.

Why Do You Need This Book?

Understanding how data structures and algorithms work in code is crucial for creating efficient and scalable apps. Swift’s Standard Library has a small set of general purpose collection types, yet they don’t give you what you need for every case.

Moreover, you’ll find these concepts helpful for your professional and personal development as a developer.

When you interview for a software engineering position, chances are that you’ll be tested on data structures and algorithms. Having a strong foundation in data structures and algorithms is the “bar” for many companies with software engineering positions.

Knowing the strategies used by algorithms to solve tricky problems gives you ideas for improvements you can make to your own code. Knowing more data structures than just the standard array and dictionary also gives you a bigger collection of tools that you can use to build your own apps.

Here’s what’s contained in the full release of the book:

Section I: Introduction

  • Chapter 1: Why Learn Data Structures & Algorithms?: Data structures are a well-studied area, and the concepts are language agnostic; a data structure from C is functionally and conceptually identical to the same data structure in any other language, such as Swift. At the same time, the high-level expressiveness of Swift make it an ideal choice for learning these core concepts without sacrificing too much performance.
  • Chapter 2: Swift Standard Library: Before you dive into the rest of this book, you’ll first look at a few data structures that are baked into the Swift language. The Swift standard library refers to the framework that defines the core components of the Swift language. Inside, you’ll find a variety of tools and types to help build your Swift apps.

Section II: Elementary Data Structures

  • Chapter 3: Linked List: A linked list is a collection of values arranged in a linear unidirectional sequence. A linked list has several theoretical advantages over contiguous storage options such as the Swift Array, including constant time insertion and removal from the front of the list, and other reliable performance characteristics.
  • Chapter 5: Stacked Data Structure: The stack data structure is identical in concept to a physical stack of objects. When you add an item to a stack, you place it on top of the stack. When you remove an item from a stack, you always remove the topmost item. Stacks are useful, and also exceedingly simple. The main goal of building a stack is to enforce how you access your data.
  • Chapter 7: Queues: Lines are everywhere, whether you are lining up to buy tickets to your favorite movie, or waiting for a printer machine to print out your documents. These real-life scenarios mimic the queue data structure. Queues use first-in-first-out ordering, meaning the first element that was enqueued will be the first to get dequeued. Queues are handy when you need to maintain the order of your elements to process later.

  • Easy-to-understand examples show key concepts, such as trees!

Section III: Trees

  • Chapter 9: Trees: The tree is a data structure of profound importance. It is used to tackle many recurring challenges in software development, such as representing hierarchical relationships, managing sorted data, and facilitating fast lookup operations. There are many types of trees, and they come in various shapes and sizes.
  • Chapter 11: Binary Trees: In the previous chapter, you looked at a basic tree where each node can have many children. A binary tree is a tree where each node has at most two children, often referred to as the left and right children. Binary trees serve as the basis for many tree structures and algorithms. In this chapter, you’ll build a binary tree and learn about the three most important tree traversal algorithms.
  • Chapter 13: Binary Search Trees: A binary search tree facilitates fast lookup, addition, and removal operations. Each operation has an average time complexity of O(log n), which is considerably faster than linear data structures such as arrays and linked lists.
  • Chapter 15: AVL Trees: In the previous chapter, you learned about the O(log n) performance characteristics of the binary search tree. However, you also learned that unbalanced trees can deteriorate the performance of the tree, all the way down to O(n). In 1962, Georgy Adelson-Velsky and Evgenii Landis came up with the first self-balancing binary search tree: the AVL Tree.

  • Helpful visuals demonstrate how to organize and sort data!

  • Chapter 17: Tries: The trie (pronounced as “try”) is a tree that specializes in storing data that can be represented as a collection, such as English words. The benefits of a trie are best illustrated by looking at it in the context of prefix matching, which is what you’ll do in this chapter.
  • Chapter 19: Binary Search: Binary search is one of the most efficient searching algorithms with a time complexity of O(log n). This is comparable with searching for an element inside a balanced binary search tree. To perform a binary search, the collection must be able to perform index manipulation in constant time, and must be sorted.
  • Chapter 21: The Heap Data Structure: A heap is a complete binary tree, also known as a binary heap, that can be constructed using an array. Heaps come in two flavors: Max heaps and Min heaps. Have you seen the movie Toy Story, with the claw machine and the squeaky little green aliens? Imagine that the claw machine is operating on your heap structure, and will always pick the minimum or maximum value, depending on the flavor of heap.
  • Chapter 23: Priority Queue: Queues are simply lists that maintain the order of elements using first-in-first-out (FIFO) ordering. A priority queue is another version of a queue that, instead of using FIFO ordering, dequeues elements in priority order. A priority queue is especially useful when you need to identify the maximum or minimum value given a list of elements.

Section IV: Sorting Algorithms

  • Chapter 25: O(n²) Sorting Algorithms: O(n²) time complexity is not great performance, but the sorting algorithms in this category are easy to understand and useful in some scenarios. These algorithms are space efficient; they only require constant O(1) additional memory space. In this chapter, you’ll be looking at the bubble sort, selection sort, and insertion sort algorithms.us shapes and sizes.
  • Chapter 27: Merge Sort: In this chapter, you’ll look at a completely different model of sorting. So far, you’ve been relying on comparisons to determine the sorting order. Radix sort is a non-comparative algorithm for sorting integers in linear time. There are multiple implementations of radix sort that focus on different problems. To keep things simple, in this chapter you’ll focus on sorting base 10 integers while investigating the least significant digit (LSD) variant of radix sort.
  • Chapter 29: Radix Sort: A binary search tree facilitates fast lookup, addition, and removal operations. Each operation has an average time complexity of O(log n), which is considerably faster than linear data structures such as arrays and linked lists.
  • Chapter 31: Heapsort: Heapsort is another comparison-based algorithm that sorts an array in ascending order using a heap. This chapter builds on the heap concepts presented in Chapter 21, “The Heap Data Structure.” Heapsort takes advantage of a heap being, by definition, a partially sorted binary tree.
  • Chapter 33: Quicksort: Quicksort is another divide and conquer technique that introduces the concept of partitions and a pivot to implement high performance sorting. You‘ll see that while it is extremely fast for some datasets, for others it can be a bit slow.

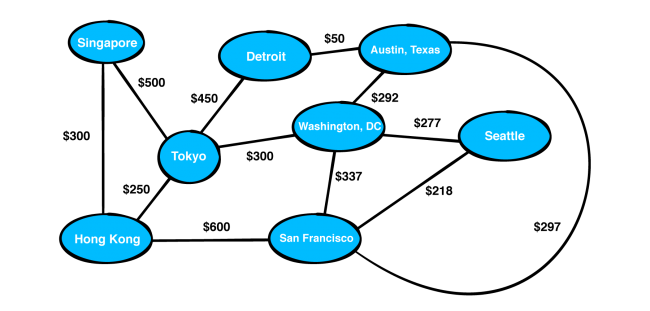
Real-world examples help you apply the book’s concepts in a concrete and relevant way!

Section V: Graphs

  • Chapter 35: Graphs: What do social networks have in common with booking cheap flights around the world? You can represent both of these real-world models as graphs! A graph is a data structure that captures relationships between objects. It is made up of vertices connected by edges. In a weighted graph, every edge has a weight associated with it that represents the cost of using this edge. This lets you choose the cheapest or shortest path between two vertices.
  • Chapter 37: Breadth-First Search: In the previous chapter, you explored how graphs can be used to capture relationships between objects. Several algorithms exist to traverse or search through a graph’s vertices. One such algorithm is the breadth-first search algorithm, which can be used to solve a wide variety of problems, including generating a minimum spanning tree, finding potential paths between vertices, and finding the shortest path between two vertices.
  • Chapter 39: Depth-First Search: In the previous chapter, you looked at breadth-first search where you had to explore every neighbor of a vertex before going to the next level. In this chapter, you will look at depth-first search, which has applications for topological sorting, detecting cycles, path finding in maze puzzles, and finding connected components in a sparse graph.
  • Chapter 41: Dijkstra’s Algorithm: Have you ever used the Google or Apple Maps app to find the shortest or fastest from one place to another? Dijkstra’s algorithm is particularly useful in GPS networks to help find the shortest path between two places. Dijkstra’s algorithm is a greedy algorithm, which constructs a solution step-by-step, and picks the most optimal path at every step.
  • Chapter 43: Prim’s Algorithm: In previous chapters, you’ve looked at depth-first and breadth-first search algorithms. These algorithms form spanning trees. In this chapter, you will look at Prim’s algorithm, a greedy algorithm used to construct a minimum spanning tree. A minimum spanning tree is a spanning tree with weighted edges where the total weight of all edges is minimized. You’ll learn how to implement a greedy algorithm to construct a solution step-by-step, and pick the most optimal path at every step.

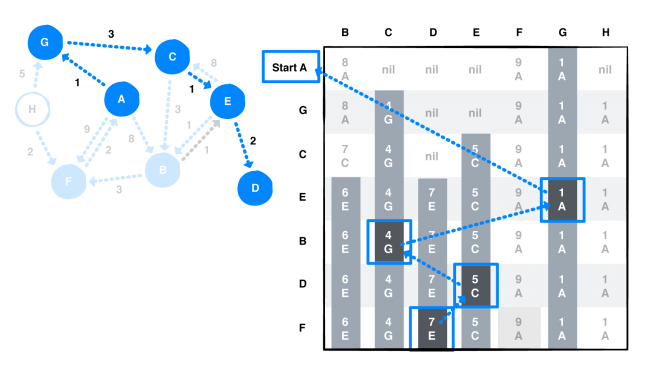
The book moves beyond fundamentals to more advanced concepts, such as Dijkstra’s Algorithm!

Data Structures and Algorithms in Swift will teach you how to implement the most popular and useful data structures, and when and why you should use one particular data structure or algorithm over another.

This set of basic data structures and algorithms will serve as an excellent foundation for building more complex and special-purpose constructs. And the high-level expressiveness of Swift makes it an ideal choice for learning these core concepts without sacrificing performance.

Get your own copy:

Questions about the book? Ask them in the comments below!

The post Data Structures & Algorithms in Swift Full Release Now Available! appeared first on Ray Wenderlich.



from Ray Wenderlich https://ift.tt/2uIGcGY

Comments

Post a Comment

Popular posts from this blog

Fitting Text to a Container

There are a number of ways to go about putting some text in a container and having it size itself to fill that container. There are different technologies we can use and different considerations to think about. Let us count the ways. Magic Number it with viewport units If you set type with vw (viewport width) units, you can find an exact number where the text pretty closely fits the container and doesn't break as you resize. I'd call this a magic number . In this case, font-size: 25.5vw; works down to a 320px viewport, but still will break much lower than that. See the Pen Fitted Text with Viewport Units by Chris Coyier ( @chriscoyier ) on CodePen . This is kind of a less exotic version of fluid typography , which involves more of a sprinkling of viewport units and min/max sizes. FitText Dave Rupert's FitText is up for the job. You still need a bit of a magic number to get the sizing just right for any particular job: See the Pen Fitted Text with FitText by Ch
Read more

GLKit Tutorial for iOS: Getting started with OpenGL ES

Image
Update note : This tutorial has been updated to Swift 4.1 and Xcode 9.3 by Felipe Laso-Marsetti . The original tutorial was written by Ray Wenderlich . If you’re interested in graphics programming, chances are that you’ve read about OpenGL, which remains the most-adopted API from a hardware and software perspective. Apple has developed a framework called GLKit to help developers create apps that leverage OpenGL and to abstract boilerplate code. It also allows developers to focus on drawing, not on getting the project set up. You’ll learn how all of this works in this GLKit tutorial for iOS. GLKit provides functionality in four areas: Views and View Controllers : These abstract much of the boilerplate code that GLKit uses to set up a basic OpenGL ES (Embedded Systems) project. Effects : These implement common shading behaviors and are a handy way of setting up basic lighting, shading, reflection mapping and skybox effects. Math : Provides helpers and functions for common math
Read more